Research Overview
Our research is motivated by the need to understand how the characteristics of precipitation and atmospheric circulations respond to climate change.Mean and extreme precipitation
Climate models suggest that both global mean precipitation and the intensity of precipitation extremes will increase in a warmer climate. Local decreases in precipitation are also expected in certain regions. Quantifying the expected changes in precipitation and in intense precipitation events is a major challenge. We are endeavoring to understand the physical basis for changes in precipitation and its extremes (including rainfall and snowfall) using simulations, theory, and observations. Our results highlight the need to better understand changes in precipitation extremes in the tropics and changes in mean precipitation over land.
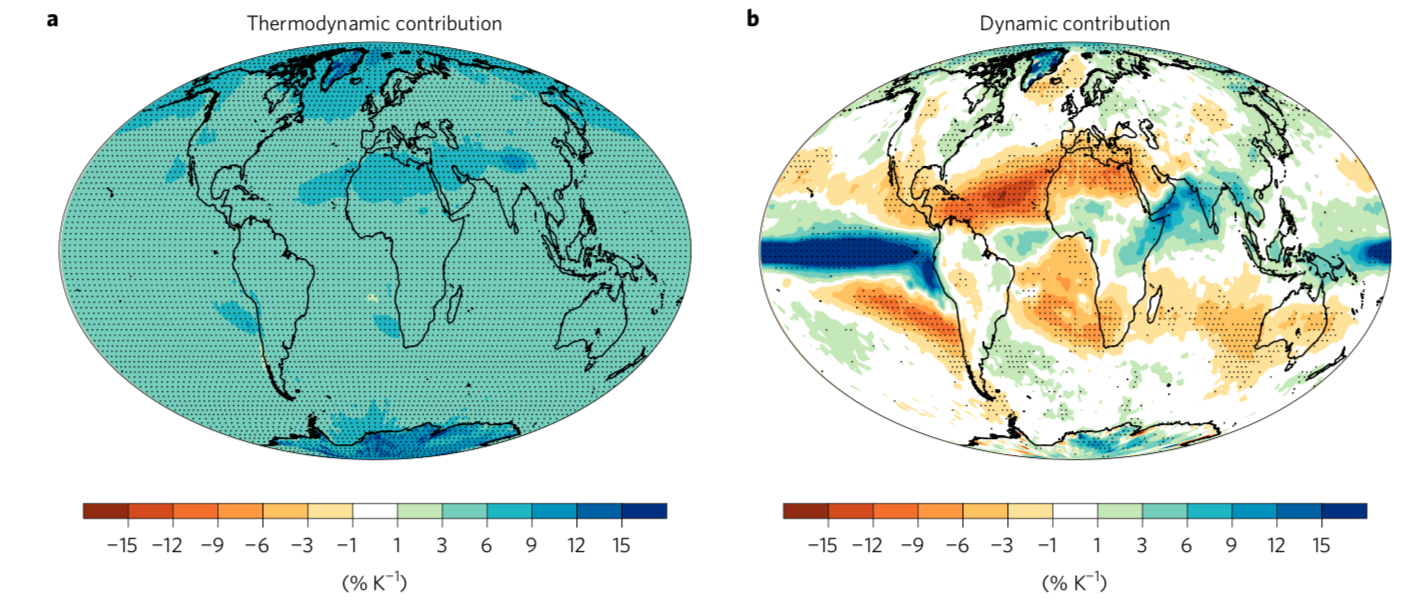
The general circulation and water vapor
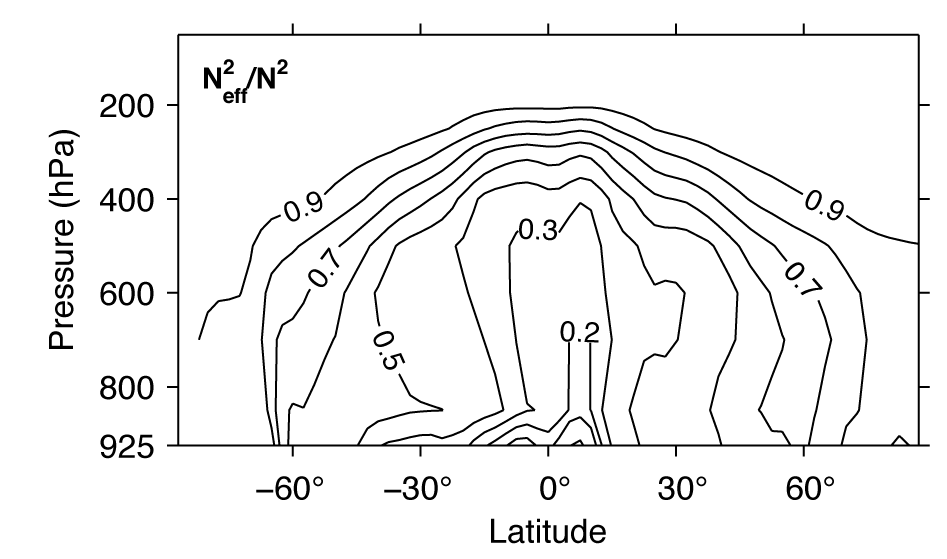
The amount of water vapor in the atmosphere responds sensitively to changes in temperature; it increases by over 20% for a 3K rise in temperature if the relative humidity remains approximately constant. Climate model simulations do predict changes in the distribution of relative humidity, but the overall change is relatively small in the vertical average. This has implications for many aspects of atmospheric dynamics when considering global warming or very warm past climates. An outstanding challenge involves fully incorporating the effect of water vapor and latent heat release into theories of how, for example, the extent of the Hadley cell, the extratropical storm track position, or the strength of extratropical storms change as climate changes. One promising approach for problems involving large-scale eddies is to use an effective static stability that accounts for the asymmetry in latent heating between downward and upward motions.
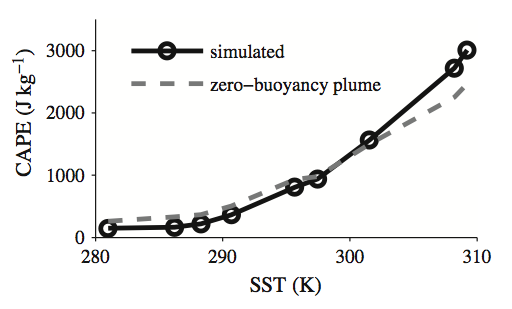
Moist convection
Moist convection plays a key role in helping to set the mean state of the tropical troposphere, and it is also a basic aspect of weather in both the tropics and midlatitudes. Climate models suggest that the convective available potential energy (CAPE) increases with warming, with implications for convective updraft velocities and severe weather. Recent studies with cloud-system resolving models show that CAPE also increases with warming in the idealized setting of radiative convective equilibrium (Fig. 3). Visualizations of our simulations illustrate that moist convection is deeper and faster at higher temperatures. We are interested in better understanding the increases in CAPE, their effect on moist convection, and the behavior of moist convection in different climates more generally.
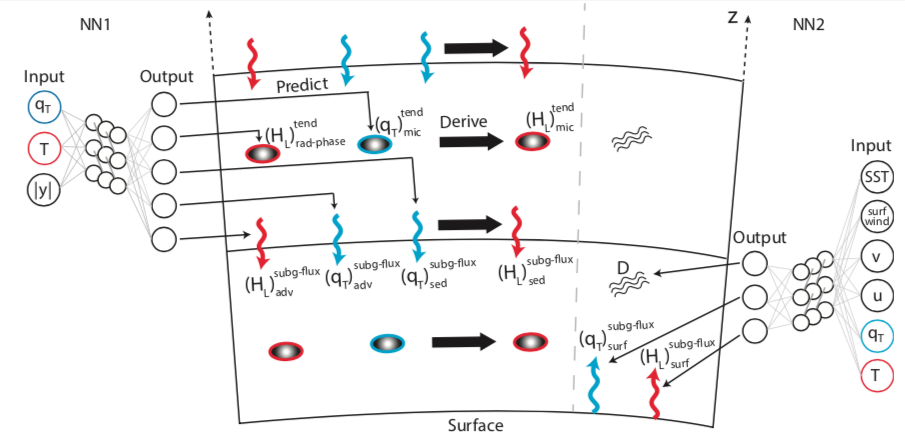
Using machine learning to develop new parameterizations for climate models
Much of the uncertainty in climate-model projections of precipitation comes from the need to parameterize subgrid processes such as atmospheric convection. We are exploring the use of machine learning to develop new parameterizations that are trained on high-resolution simulations that can faithfully represent these subgrid processes. We aim to develop parameterizations that are robust, stable and physically consistent. See Yuval and O'Gorman 2020 and Yuval, O'Gorman and Hill 2021 for further information.