Effective static stability
This webpage gives a description of the effective static stability of O'Gorman, JAS, 68, 75-90, 2011 [1] and its application to the atmosphere and model simulations. A Matlab script is provided that evaluates the effective static stability based on vertical profiles of atmospheric properties. References to related papers are also given.Introduction
The effective static stability replaces the dry static stability for dynamical problems involving eddies in a moist atmosphere. It may be considerably smaller than the dry static stability (Fig. 1), although it is not reduced to zero (even when lapse rates are moist adiabatic) as long as there are non-precipitating regions of the eddy.
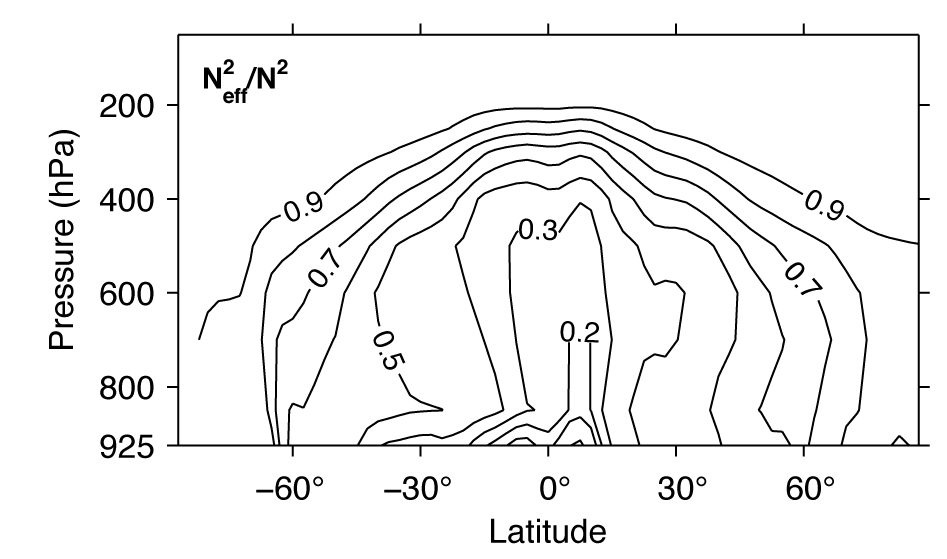
Applications and Testing
The effective static stability has been applied to better understand the strength and length scale of extratropical eddies [1,3], the extratropical thermal stratification [1] and land-ocean warming contrast [5,6], the deepening rates of extratropical cyclones [4,7], the extent of the Hadley cells [1,8], and moist Eliassen-Palm fluxes and their connection to the surface westerlies [9]. Fig. 2 shows an example of its use to estimate the eddy length scale in simulations over a wide range of climates [1]. The effective static stability is used in place of the dry static stability in the Rossby radius of deformation to give a simple estimate of the eddy length scale that is applicable to a moist atmosphere.

The effective static stability has been directly tested by removing the hydrological cycle in an idealized GCM and replacing the dry static stability in the thermodynamic equation with the effective static stability. The resulting simulations (with specified zonal-mean fields to allow for comparison) have eddy statistics that are similar to the eddy statistics in a control simulation with a full hydrological cycle (see Fig. 8 of reference [1]).
Definition
The effective static stability is defined as
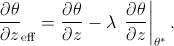
where θ is dry potential temperature, z is height, θ* is saturated equivalent potential temperature, and λ is the asymmetry parameter discussed below. The quantity ∂θ/∂z|θ* is a function of temperature and pressure that can be easily evaluated in terms of the moist adiabatic lapse rate (see Matlab script for details).
Asymmetry Parameter λ
The parameter λ measures the asymmetry of vertical motions between upwards and downwards. A value of λ=0.5 corresponds to statistical symmetry between upwards and downwards motion (as in dry quasigeostrophic theory), whereas λ=1 corresponds to infinitely fast and narrow updrafts. The asymmetry parameter is calculated from the statistics of the vertical pressure velocity ω as
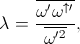
where the overbar refers to a mean, ω' is the eddy vertical velocity, and ω↑ is the upward vertical velocity (set to zero for downward motion).
The asymmetry parameter has values of approximately λ=0.6 in midlatitudes when evaluated using NCEP2 winds, and it doesn't change greatly over the seasonal cycle in NCEP2 or under global warming in climate-model simulations [1,3,10]. It has higher values of λ=0.74 in baroclinic lifecycles simulated by WRF [4], although it does not seem to depend strongly on horizontal or vertical spatial resolution in either the WRF simulations or in simulations with an idealized GCM [10].
Matlab script
This Matlab script evaluates the effective static stability in pressure coordinates given 1d vertical profiles of temperature, pressure, and the asymmetry parameter λ. If λ is not specified, a default value of λ=0.6 is assumed that is appropriate for the midlatitudes.
Download: eff_stat_stab.m
Related publications and theses:
[1] O'Gorman, P. A.: The effective static stability experienced by eddies in a moist atmosphere Journal of the Atmospheric Sciences 68, 75-90, 2011
[2] Kanamitsu, M. et al: NCEP-DOE AMIP-II Reanalysis (R-2) Bull. Amer. Meteor. Soc. 83, 1631-1643, 2002
[3] Mooring, T. A.: Changes in atmospheric eddy length with the seasonal cycle and global warming MIT Undergraduate Thesis, 2011
[4] Booth, J. F., Polvani, L. M., O'Gorman, P. A., & Wang, S.: Effective stability in a moist baroclinic wave Atmospheric Science Letters 16, 56-62, 2015
[5] Byrne, M. P. & O'Gorman, P. A.: Land-ocean warming contrast over a wide range of climates: convective quasi-equilibrium theory and idealized simulations Journal of Climate 26, 4000-4016, 2013
[6] Byrne, M. P.: Land-ocean contrasts under climate change MIT PhD Thesis, 2014
[7] Pfahl, S., O'Gorman, P. A. & Singh, M. S.: Midlatitude cyclones in idealized simulations of changed climates Journal of Climate 28, 9373-9392, 2015
[8] Levine, X. J., and Schneider, T.: Baroclinic eddies and the extent of the Hadley circulation: An idealized GCM study Journal of the Atmospheric Sciences 72, 2744-2761, 2015
[9] Dwyer, J. G. and O'Gorman, P. A.: Moist formulations of the Eliassen-Palm flux and their connection to the surface westerlies Journal of the Atmospheric Sciences 74, 513-530
[10] O'Gorman, P. A., Merlis, T. M. and Singh, M. S.: Increase in the skewness of extratropical vertical velocities with climate warming: fully nonlinear simulations versus moist baroclinic instability Quarterly Journal of the Royal Meteorological Society doi: 10.1002/qj.3195
Acknowledgments
Much of this material is based upon work supported by the National Science Foundation under Grant Number AGS-1148594. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author and do not necessarily reflect the views of the National Science Foundation.